Enigma machine

The Enigma
cipher machine

An Enigma machine is any of a family of related electro-mechanical rotor cipher machines used for the encryption and decryption of secret messages. Enigma was invented by German engineer Arthur Scherbius at the end of World War I.[1] The early models were used commercially from the early 1920s, and adopted by military and government services of several countries — most notably by Nazi Germany before and during World War II.[2] Several different Enigma models were produced, but the German military models are the ones most commonly discussed.

In December 1932, the Polish Cipher Bureau first broke Germany's military Enigma ciphers. Five weeks before the outbreak of World War II, on 25 July 1939, in Warsaw, they presented their Enigma-decryption techniques and equipment to French and British military intelligence.[3][4] Thanks to this,[5] during the war, Allied codebreakers were able to decrypt a vast number of messages that had been enciphered using the Enigma. The intelligence gleaned from this source, codenamed "Ultra" by the British, was a substantial aid to the Allied war effort.[6]

The exact influence of Ultra on the course of the war is debated; an oft-repeated assessment is that decryption of German ciphers hastened the end of the European war by two years.[7][8][9] Winston Churchill told Britain's King George VI after World War II: "It was thanks to Ultra that we won the war."[10]

Although Enigma had some cryptographic weaknesses, in practice it was only in combination with procedural flaws, operator mistakes, captured key tables and hardware, that Allied cryptanalysts were able to be so successful.[11]

Contents

Description

Like other rotor machines, the Enigma machine is a combination of mechanical and electrical subsystems. The mechanical subsystem consists of a keyboard; a set of rotating disks called rotors arranged adjacently along a spindle; and one of various stepping components to turn one or more of the rotors with each key press.

Electrical pathway

The mechanical parts act in such a way as to form a varying electrical circuit. When a key is pressed, a circuit is completed with current flowing through the various components in their current configuration and ultimately lighting one of the display lamps, indicating the output letter. For example, when encrypting a message starting ANX…, the operator would first press the A key, and the Z lamp might light, so Z would be the first letter of the ciphertext. The operator would next press N, and then X in the same fashion, and so on.

The detailed operation of Enigma is shown in the wiring diagram to the right. To simplify the example, only four components of a complete Enigma machine are shown. In reality, there are 26 lamps and keys, rotor wirings inside the rotors (of which there were either three or four) and between six and ten plug leads.

Current flowed from the battery (1) through a depressed bi-directional keyboard switch (2) to the plugboard (3). Next, it passed through the (unused in this instance, so shown closed) plug (3) via the entry wheel (4), through the wiring of the three (Wehrmacht Enigma) or four (Kriegsmarine M4 and Abwehr variants) installed rotors (5), and entered the reflector (6). The reflector returned the current, via an entirely different path, back through the rotors (5) and entry wheel (4), proceeding through plug 'S' (7) connected with a cable (8) to plug 'D', and another bi-directional switch (9) to light the appropriate lamp.[12]

The repeated changes of electrical path through an Enigma scrambler, implemented a polyalphabetic substitution cipher which provided Enigma's high security. The diagram on the left shows how the electrical pathway changed with each key depression, which caused rotation of at least the right hand rotor. Current passed into the set of rotors, into and back out of the reflector, and out through the rotors again. The greyed-out lines are some other possible paths within each rotor; these are hard-wired from one side of each rotor to the other. Letter A encrypts differently with consecutive key presses, first to G, and then to C. This is because the right hand rotor has stepped, sending the signal on a completely different route; eventually other rotors will also step with a key press.

Rotors

Main article: Enigma rotor details

The rotors (alternatively wheels or drums, Walzen in German) formed the heart of an Enigma machine. Each rotor was a disc approximately 10 cm (3.9 in) in diameter made from hard rubber or bakelite with brass spring-loaded pins on one face arranged in a circle; on the other side are a corresponding number of circular electrical contacts. The pins and contacts represent the alphabet — typically the 26 letters A–Z (this will be assumed for the rest of this description). When the rotors were mounted side-by-side on the spindle, the pins of one rotor rest against the contacts of the neighbouring rotor, forming an electrical connection. Inside the body of the rotor, 26 wires connected each pin on one side to a contact on the other in a complex pattern. Most of the rotors were identified by Roman numerals and each issued copy of rotor I was wired identically to all others. The same was true of the special thin beta and gamma rotors used in the M4 naval variant.

By itself, a rotor will perform only a very simple type of encryption — a simple substitution cipher. For example, the pin corresponding to the letter E might be wired to the contact for letter T on the opposite face, and so on. The Enigma's complexity, and cryptographic security, came from using several rotors in series (usually three or four) and the regular stepping movement of the rotors, thus implementing a poly-alphabetic substitution cipher.

When placed in an Enigma, each rotor can be set to one of 26 possible positions. When inserted, it can be turned by hand using the grooved finger-wheel which protrudes from the internal Enigma cover when closed. So that the operator can know the rotor's position, each had an alphabet tyre (or letter ring) attached to the outside of the rotor disk, with 26 characters (typically letters); one of these could be seen through the window, thus indicating the rotational position of the rotor. In early Enigma models, the alphabet ring was fixed to the rotor disk. An improvement introduced in later variants was the ability to adjust the alphabet ring relative to the rotor disk. The position of the ring was known as the Ringstellung ("ring setting"), and was a part of the initial setting of an Enigma prior to an operating session. In modern terms it was a part of the initialization vector.

The rotors each contained a notch (more than one for some rotors) which was used to control rotor stepping. In the military variants, the notches are located on the alphabet ring.

The Army and Air Force Enigmas were used with several rotors; when first issued, there were only three. On 15 December 1938, this changed to five, from which three were chosen for insertion in the machine for a particular operating session. Rotors were marked with Roman numerals to distinguish them: I, II, III, IV and V, all with single notches located at different points on the alphabet ring. This variation was probably intended as a security measure, but ultimately allowed the Polish Clock Method and British Banburismus attacks.

The Naval version of the Wehrmacht Enigma had always been issued with more rotors than the other services: at first six, then seven, and finally eight. The additional rotors were marked VI, VII and VIII, all with different wiring, and had two notches cut into them resulting in a more frequent turnover. The four-rotor Naval Enigma (M4) machine accommodated an extra rotor in the same space as the three-rotor version. This was accomplished by replacing the original reflector with a thinner one and by adding a special, also thin, fourth rotor. That fourth rotor was one of two types, Beta or Gamma, and never stepped, but it could be manually set to any of its 26 possible positions, one of which made the machine perform identically to the three-rotor machine.

Stepping

To avoid merely implementing a simple (and easily breakable) substitution cipher, every key press caused one or more rotors to step by one twenty-sixth of a full rotation, before the electrical connections were made. This changed the substitution alphabet used for encryption, ensuring that the cryptographic substitution was different at each new rotor position, producing a more formidable polyalphabetic substitution cipher. The stepping mechanism varied slightly from model to model. The right-hand rotor stepped once with each key stroke, and other rotors stepped less frequently.

Turnover

The advancement of a rotor other than the left-hand one was called a turnover by the cryptanalysts at Bletchley Park. This was achieved by a ratchet and pawl mechanism. Each rotor had a ratchet with 26 teeth and every time a key was pressed, the set of spring-loaded pawls moved forward in unison, trying to engage with a ratchet. The alphabet ring of the rotor to the right normally prevented this. As this ring rotated with its rotor, a notch machined into it would eventually align itself with the pawl, allowing it to engage with the ratchet, and advance the rotor on its left. The right-hand pawl, having no rotor and ring to its right, stepped its rotor with every key depression.[13] For a single-notch rotor in the right-hand position, the middle rotor stepped once for every 26 steps of the right-hand rotor. Similarly for rotors two and three. For a two-notch rotor, the rotor to its left would turn over twice for each rotation.

The first five rotors to be introduced (I–V) contained one notch each, while the additional naval rotors VI, VII and VIII each had two notches. The position of the notch on each rotor was determined by the letter ring which could be adjusted in relation to the core containing the interconnections. The points on the rings at which they caused the next wheel to move were as follows.[14]

Position of turnover notches
Rotor Turnover position(s) BP mnemonic
I R Royal
II F Flags
III W Wave
IV K Kings
V A Above
VI, VII and VIII A and N

The design also included a feature known as double-stepping. This was enabled due to each pawl being aligned with both the ratchet of its rotor and the rotating notched ring of the neighbouring rotor. If a pawl was allowed to engage with a ratchet through alignment with a notch, as it moved forward it would push against both the ratchet and the notch, advancing both rotors at the same time. In a three-rotor machine, the double-stepping would affect rotor two only. This, if in moving forward allowed the ratchet of rotor three to be engaged, would move again on the subsequent keystroke, thus resulting in two consecutive steps. Rotor two also pushes rotor one forward after 26 of its steps, but as rotor one moves forward with every keystroke anyway, there is no double-stepping.[13] This double-stepping caused the rotors to deviate from odometer-style regular motion.

With three wheels and only single notches in the first and second wheels, the machine had a period of 26 × 25 × 26 = 16,900 (not 26 × 26 × 26 because of the double-stepping of the second rotor).[13] Historically, messages were limited to a few hundred letters, and so there was no chance of repeating any net combined rotor position during a single message session, and so cryptanalysts were denied a valuable clue to the substitution used.

To make room for the Naval fourth rotors, Beta and Gamma (introduced in 1942), the reflector was changed, by making it much thinner. The special fourth rotors fit into the space made available. No changes were made to the rest of the mechanism, which eased the changeover to the new mode of operation. Since there were only three pawls, the fourth rotor never stepped, but could be manually set into one of its 26 possible positions.

A device that was designed, but not implemented before the war's end, was the Lückenfüllerwalze (gap-fill wheel) which implemented irregular stepping. It allowed field configuration of notches in all 26 positions. If the number of notches was a relative prime of 26 and the number of notches were different for each wheel, the stepping would be more unpredictable. Like the Umkehrwalze-D it also allowed the internal wiring to be reconfigured.[15]

Entry wheel

The current entry wheel (Eintrittswalze in German), or entry stator, connects the plugboard, if present, or otherwise the keyboard and lampboard, to the rotor assembly. While the exact wiring used is of comparatively little importance to the security, it proved an obstacle in the progress of Polish cryptanalyst Marian Rejewski during his deduction of the rotor wirings. The commercial Enigma connects the keys in the order of their sequence on the keyboard: Q\rightarrowA, W\rightarrowB, E\rightarrowC and so on. However, the military Enigma connects them in straight alphabetical order: A\rightarrowA, B\rightarrowB, C\rightarrowC, and so on. It took an inspired piece of guesswork for Rejewski to realise the modification.

Reflector

With the exception of the early Enigma models A and B, the last rotor came before a reflector (German: Umkehrwalze, meaning reversal rotor), a patented feature distinctive of the Enigma family amongst the various rotor machines designed in the period. The reflector connected outputs of the last rotor in pairs, redirecting current back through the rotors by a different route. The reflector ensured that Enigma is self-reciprocal: conveniently, encryption was the same as decryption. However, the reflector also gave Enigma the property that no letter ever encrypted to itself. This was a severe conceptual flaw and a cryptological mistake subsequently exploited by codebreakers.

In the commercial Enigma model C, the reflector could be inserted in one of two different positions. In Model D, the reflector could be set in 26 possible positions, although it did not move during encryption. In the Abwehr Enigma, the reflector stepped during encryption in a manner like the other wheels.

In the German Army and Air Force Enigma, the reflector was fixed and did not rotate; there were four versions. The original version was marked A, and was replaced by Umkehrwalze B on 1 November 1937. A third version, Umkehrwalze C was used briefly in 1940, possibly by mistake, and was solved by Hut 6.[16] The fourth version, first observed on 2 January 1944, had a rewireable reflector, called Umkehrwalze D, allowing the Enigma operator to alter the connections as part of the key settings.

Plugboard

The plugboard (Steckerbrett in German) permitted variable wiring that could be reconfigured by the operator (visible on the front panel of Figure 1; some of the patch cords can be seen in the lid). It was introduced on German Army versions in 1930, and was soon adopted by the Navy as well. The plugboard contributed a great deal to the strength of the machine's encryption: more than an extra rotor would have done. Enigma without a plugboard (known as unsteckered Enigma) can be solved relatively straightforwardly using hand methods; these techniques are generally defeated by the addition of a plugboard, and Allied cryptanalysts resorted to special machines to solve it.

A cable placed onto the plugboard connected letters up in pairs; for example, E and Q might be a steckered pair. The effect was to swap those letters before and after the main rotor scrambling unit. For example, when an operator presses E, the signal was diverted to Q before entering the rotors. Several such steckered pairs, up to 13, might be used at one time. However, normally only 10 pairs were used at any one time.

Current flowed from the keyboard through the plugboard, and proceeded to the entry-rotor or Eintrittswalze. Each letter on the plugboard had two jacks. Inserting a plug disconnected the upper jack (from the keyboard) and the lower jack (to the entry-rotor) of that letter. The plug at the other end of the crosswired cable was inserted into another letter's jacks, thus switching the connections of the two letters.

Accessories

A number of additional features were produced to make various Enigma machines more secure or more convenient to use.[17]

One feature that was used on some M4 Enigmas was the Schreibmax, a small printer which could print the 26 letters on a narrow paper ribbon. This did away with the need for a second operator to read the lamps and write the letters down. The Schreibmax was placed on top of the Enigma machine and was connected to the lamp panel. To install the printer, the lamp cover and all light bulbs had to be removed. Besides its convenience, it could improve operational security; the printer could be installed remotely such that the signal officer operating the machine no longer had to see the decrypted plaintext information.

Another accessory was the remote lamp panel Fernlesegerät. For machines equipped with the extra panel, the wooden case of the Enigma was wider and could store the extra panel. There was a lamp panel version that could be connected afterwards, but that required, just as with the Schreibmax, that the lamp panel and lightbulbs be removed.[12] The remote panel made it possible for a person to read the decrypted plaintext without the operator seeing it.

In 1944, the Luftwaffe introduced a plugboard switch, called the Uhr (clock). There was a little box, containing a switch with 40 positions. It replaced the standard plugs. After connecting the plugs, as determined in the daily key sheet, the operator turned the switch into one of the 40 positions, each position producing a different combination of plug wiring. Most of these plug connections were, unlike the default plugs, not pair-wise.[12] In one switch position, the Uhr did not swap any letters, but simply emulated the 13 stecker wires with plugs.

Mathematical analysis

The Enigma transformation for each letter can be specified mathematically as a product of permutations.[18] Assuming a three-rotor German Army/Air Force Enigma, let 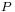\scriptstyle P denote the plugboard transformation, 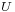\scriptstyle U denote that of the reflector, and 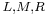\scriptstyle L, M, R denote those of the left, middle and right rotors respectively. Then the encryption 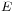\scriptstyle E can be expressed as

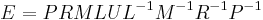E = PRMLUL^{-1}M^{-1}R^{-1}P^{-1}.

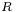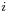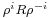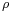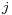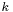After each key press, the rotors turn, changing the transformation. For example, if the right hand rotor \scriptstyle R is rotated \scriptstyle i positions, the transformation becomes \scriptstyle\rho^iR\rho^{-i}, where \scriptstyle\rho is the cyclic permutation mapping A to B, B to C, and so forth. 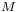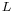Similarly, the middle and left-hand rotors can be represented as \scriptstyle j and \scriptstyle k rotations of \scriptstyle M and \scriptstyle L. The encryption transformation can then be described as

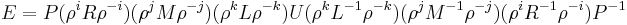E = P(\rho^iR\rho^{-i})(\rho^{j}M\rho^{-j})(\rho^{k}L\rho^{-k})U(\rho^kL^{-1}\rho^{-k})(\rho^{j}M^{-1}\rho^{-j})(\rho^{i}R^{-1}\rho^{-i})P^{-1}.

Operation

In use, the Enigma required a list of daily key settings as well as a number of auxiliary documents. The procedures for German Naval Enigma were more elaborate and more secure than the procedures used in other services. The Navy codebooks were also printed in red, water-soluble ink on pink paper so that they could easily be destroyed if they were at risk of being seized by the enemy. The codebook to the right was taken from captured German submarine U-505.

In German military usage, communications were divided up into a number of different networks, all using different settings for their Enigma machines. These communication nets were termed keys at Bletchley Park, and were assigned code names, such as Red, Chaffinch, and Shark. Each unit operating on a network was assigned a settings list for its Enigma for a period of time. For a message to be correctly encrypted and decrypted, both sender and receiver had to set up their Enigma in the same way; the rotor selection and order, the starting position and the plugboard connections must be identical. All these settings (together the key in modern terms) must have been established beforehand, and were distributed in codebooks.

An Enigma machine's initial state, the cryptographic key, has several aspects:

Note that although the ring settings (ringstellung) were a required part of the setup, they did not actually affect the message encryption because the rotors were positioned independently of the rings. The ring settings were only necessary to determine the initial rotor position based on the message setting which was transmitted at the beginning of a message, as described in the "Indicators" section, below. Once the receiver had set his rotors to the indicated positions, the ring settings no longer played any role in the encryption.

In modern cryptographic language, the ring settings did not actually contribute entropy to the key used for encrypting the message. Rather, the ring settings were part of a separate key (along with the rest of the setup such as wheel order and plug settings) used to encrypt an initialization vector for the message. The session key consisted of the complete setup except for the ring settings, plus the initial rotor positions chosen arbitrarily by the sender (the message setting). The important part of this session key was the rotor positions, not the ring positions. However, by encoding the rotor position into the ring position using the ring settings, additional variability was added to the encryption of the initialization vector.

Enigma was designed to be secure even if the rotor wiring was known to an opponent, although in practice there was considerable effort to keep the wiring secret. If the wiring is secret, the total number of possible configurations has been calculated to be around 10114 (approximately 380 bits); with known wiring and other operational constraints, this is reduced to around 10²³ (76 bits).[8] Users of Enigma were confident of its security because of the large number of possibilities; it was not then feasible for an adversary to even begin to try every possible configuration in a brute force attack.

Indicator

Most of the key was kept constant for a set time period, typically a day. However, a different initial rotor position was used for each message, a concept similar to an initialisation vector in modern cryptography. The reason for this is that, were a number of messages to be encrypted with identical or near-identical settings (termed in cryptanalysis as being in depth), it would be possible to attack the messages using a statistical procedure such as Friedman's Index of coincidence.[19] The starting position for the rotors was transmitted just before the ciphertext, usually after having been enciphered. The exact method used was termed the indicator procedure. It was design weakness and operator sloppiness in these indicator procedures that were two of the main reasons that breaking Enigma messages was possible.

One of the earliest indicator procedures was used by Polish cryptanalysts to make the initial breaks into the Enigma. The procedure was for the operator to set up his machine in accordance with his settings list, which included a global initial position for the rotors (Grundstellung, meaning ground setting), AOH, perhaps. The operator turned his rotors until AOH was visible through the rotor windows. At that point, the operator chose his own, arbitrary, starting position for that particular message. An operator might select EIN, and these became the message settings for that encryption session. The operator then typed EIN into the machine, twice, to allow for detection of transmission errors. The results were an encrypted indicator—the EIN typed twice might turn into XHTLOA, which would be transmitted along with the message. Finally, the operator then spun the rotors to his message settings, EIN in this example, and typed the plaintext of the message.

At the receiving end, the operation was reversed. The operator set the machine to the initial settings and typed in the first six letters of the message (XHTLOA). In this example, EINEIN emerged on the lamps. After moving his rotors to EIN, the receiving operator then typed in the rest of the ciphertext, deciphering the message.

The weakness in this indicator scheme came from two factors. First, use of a global ground setting—this was later changed so the operator selected his initial position to encrypt the indicator, and sent the initial position in the clear. The second problem was the repetition of the indicator, which was a serious security flaw. The message setting was encoded twice, resulting in a relation between first and fourth, second and fifth, and third and sixth character. This security problem enabled the Polish Cipher Bureau to break into the pre-war Enigma system as early as 1932. However, from 1940 on, the Germans changed the procedures to increase the security.

During World War II, codebooks were only used each day to set up the rotors, their ring settings and the plugboard. For each message, the operator selected a random start position, let's say WZA, and a random message key, perhaps SXT. He moved the rotors to the WZA start position and encoded the message key SXT. Assume the result was UHL. He then set up the message key, SXT, as the start position and encrypted the message. Next, he transmitted the start position, WZA, the encoded message key, UHL, and then the ciphertext. The receiver set up the start position according to the first trigram, WZA, and decoded the second trigram, UHL, to obtain the SXT message setting. Next, he used this SXT message setting as the start position to decrypt the message. This way, each ground setting was different and the new procedure avoided the security flaw of double encoded message settings.[20]

This procedure was used by Wehrmacht and Luftwaffe only. The Kriegsmarine procedures on sending messages with the Enigma were far more complex and elaborate. Prior to encryption with the Enigma, the message was encoded using the Kurzsignalheft code book. The Kurzsignalheft contained tables to convert sentences into four-letter groups. A great many choices were included, for example, logistic matters such as refueling and rendezvous with supply ships, positions and grid lists, harbor names, countries, weapons, weather conditions, enemy positions and ships, date and time tables. Another codebook contained the Kenngruppen and Spruchschlüssel: the key identification and message key.[21]

Some details

The Army Enigma machine used only the 26 alphabet characters. Signs were replaced with rare character combinations. A space was omitted or replaced with an X. The X was generally used as point or full-stop.

Some signs were different in other parts of the armed forces. The Wehrmacht replaced a comma with ZZ and the question sign with FRAGE or FRAQ.

The Kriegsmarine replaced the comma with Y and the question sign with UD. The combination CH, as in "Acht" (eight) or "Richtung" (direction), was replaced with Q (AQT, RIQTUNG). Two, three and four zeros were replaced with CENTA, MILLE and MYRIA.

The Wehrmacht and the Luftwaffe transmitted messages in groups of five characters.

The Kriegsmarine, using the four rotor Enigma, had four-character groups. Frequently-used names or words were to be varied as much as possible. Words like Minensuchboot (minesweeper) could be written as MINENSUCHBOOT, MINBOOT, MMMBOOT or MMM354. To make cryptanalysis harder, it was forbidden to use more than 250 characters in a single message. Longer messages were divided into several parts, each using its own message key.[22][23]

History of the machine

Far from being a single design, there are numerous models and variants of the Enigma family. The earliest Enigma machines were commercial models dating from the early 1920s. Starting in the mid-1920s, the various branches of the German military began to use Enigma, making a number of changes in order to increase its security. In addition, a number of other nations either adopted or adapted the Enigma design for their own cipher machines.

Commercial Enigma

On 23 February 1918, German engineer Arthur Scherbius applied for a patent for a cipher machine using rotors and, with E. Richard Ritter, founded the firm of Scherbius & Ritter. They approached the German Navy and Foreign Office with their design, but neither was interested. They then assigned the patent rights to Gewerkschaft Securitas, who founded the Chiffriermaschinen Aktien-Gesellschaft (Cipher Machines Stock Corporation) on 9 July 1923; Scherbius and Ritter were on the board of directors.

Chiffriermaschinen AG began advertising a rotor machine — Enigma model A — which was exhibited at the Congress of the International Postal Union in 1923-1924. The machine was heavy and bulky, incorporating a typewriter. It measured 65×45×35 cm and weighed about 50 kg (110 lb).

In 1925 Enigma model B was introduced, and was of a similar construction.[24] While bearing the Enigma name, both models A and B were quite unlike later versions: they differed in physical size and shape, but also cryptographically, in that they lacked the reflector.

The reflector — an idea suggested by Scherbius's colleague Willi Korn — was first introduced in the Enigma C (1926) model. The reflector is a key feature of the Enigma machines.

Model C was smaller and more portable than its predecessors. It lacked a typewriter, relying instead on the operator reading the lamps; hence the alternative name of "glowlamp Enigma" to distinguish from models A and B.

The Enigma C quickly became extinct, giving way to the Enigma D (1927). This version was widely used, with examples going to Sweden, the Netherlands, United Kingdom, Japan, Italy, Spain, United States, and Poland.


Military Enigma

The Navy was the first branch of the German military to adopt Enigma. This version, named Funkschlüssel C ("Radio cipher C"), had been put into production by 1925 and was introduced into service in 1926.[25]

The keyboard and lampboard contained 29 letters—A-Z, Ä, Ö and Ü—which were arranged alphabetically, as opposed to the QWERTZU ordering.[26] The rotors had 28 contacts, with the letter X wired to bypass the rotors unencrypted.[27]

Three rotors were chosen from a set of five[28] and the reflector could be inserted in one of four different positions, denoted α, β, γ and δ.[29] The machine was revised slightly in July 1933.[30]

By 15 July 1928,[31] the German Army (Reichswehr) had introduced their own version of the Enigma—the Enigma G, revised to the Enigma I by June 1930.[32] Enigma I is also known as the Wehrmacht, or "Services" Enigma, and was used extensively by the German military services and other government organisations (such as the railways[33]), both before and during World War II.

The major difference between Enigma I and commercial Enigma models was the addition of a plugboard to swap pairs of letters, greatly increasing the cryptographic strength of the machine. Other differences included the use of a fixed reflector, and the relocation of the stepping notches from the rotor body to the movable letter rings.[32] The machine measured 28×34×15 cm (11 in×13.5 in×6 in) and weighed around 12 kg (26 lb).[27]

By 1930, the Army had suggested that the Navy adopt their machine, citing the benefits of increased security (with the plugboard) and easier interservice communications.[34] The Navy eventually agreed and in 1934[35] brought into service the Navy version of the Army Enigma, designated Funkschlüssel ' or M3. While the Army used only three rotors at that time, for greater security the Navy specified a choice of three from a possible five.[36]

In December 1938, the Army issued two extra rotors so that the three rotors were chosen from a set of five.[32] In 1938, the Navy added two more rotors, and then another in 1939 to allow a choice of three rotors from a set of eight.[36] In August 1935, the Air Force also introduced the Wehrmacht Enigma for their communications.[32]

A four-rotor Enigma was introduced by the Navy for U-boat traffic on 1 February 1942, called M4 (the network was known as Triton, or Shark to the Allies). The extra rotor was fitted in the same space by splitting the reflector into a combination of a thin reflector and a thin fourth rotor.

There was also a large, eight-rotor printing model, the Enigma II. In 1933 the Polish Cipher Bureau detected that it was in use for high-level military communications, but that it was soon withdrawn from use after it was found to be unreliable and to jam frequently.[37]

The Abwehr used the Enigma G (the Abwehr Enigma). This Enigma variant was a four-wheel unsteckered machine with multiple notches on the rotors. This model was equipped with a counter which incremented upon each key press, and so is also known as the "counter machine" or the Zählwerk Enigma.

Other countries also used Enigma machines. The Italian Navy adopted the commercial Enigma as "Navy Cipher D"; the Spanish also used commercial Enigma during their Civil War. British codebreakers succeeded in breaking these machines, which lacked a plugboard.[38]

The Swiss used a version of Enigma called model K or Swiss K for military and diplomatic use, which was very similar to the commercial Enigma D. The machine was broken by a number of parties, including Poland, France, Britain and the United States (the latter codenamed it INDIGO). An Enigma T model (codenamed Tirpitz) was manufactured for use by the Japanese.

It has been estimated that 100,000 Enigma machines were constructed.[39] After the end of World War II, the Allies sold captured Enigma machines, still widely considered secure, to a number of developing countries.[39]

Breaking Enigma

Main article: Cryptanalysis of the Enigma

Surviving machines

The effort to break the Enigma was not disclosed until the 1970s. Since then, interest in the Enigma machine has grown considerably and a number of Enigmas are on public display in museums around the world.

The Deutsches Museum in Munich has both the three- and four-rotor German military variants, as well as several older civilian versions. Several Enigma machines are exhibited at National Codes Centre in Bletchley Park, the Science Museum in London, at the Polish Army Museum in Warsaw, the Armémuseum (Swedish Army Museum) in Stockholm, the National Signals Museum in Finland, and at the Australian War Memorial and in the foyer of the Defence Signals Directorate, both in Canberra, Australia.

In the United States, Enigma machines can be seen at the Computer History Museum in Mountain View, California, at the National Security Agency's National Cryptologic Museum at Fort Meade, Maryland, where visitors can try their hand at encrypting messages and deciphering code, and two machines that were acquired after the capture of U-505 during World War II, are on display at the Museum of Science and Industry in Chicago, Illinois. The now-defunct San Diego "Computer Museum of America" had an Enigma in its collection, which has since been given to the San Diego State University Library.

The only Enigma machine in Canada, a Swiss Army issue Enigma-K, is in Calgary, Alberta. It is on permanent display at The Naval Museum Of Alberta inside the Military Museums Of Calgary.

A number of machines are also in private hands. Occasionally, Enigma machines are sold at auction; prices of US$40,000 are not unusual.[40][41] Replicas of the machine are available in various forms, including an exact reconstructed copy of the Naval M4 model, an Enigma implemented in electronics (Enigma-E), various computer software simulators and paper-and-scissors analogues.

A rare Abwehr Enigma machine, designated G312, was stolen from the Bletchley Park museum on 1 April 2000. In September, a man identifying himself as "The Master" sent a note demanding £25,000 and threatened to destroy the machine if the ransom was not paid. In early October 2000, Bletchley Park officials announced that they would pay the ransom but the stated deadline passed with no word from the blackmailer. Shortly afterwards, the machine was sent anonymously to BBC journalist Jeremy Paxman, but three rotors were missing.

In November 2000, an antiques dealer named Dennis Yates was arrested after telephoning The Sunday Times to arrange the return of the missing parts. The Enigma machine was returned to Bletchley Park after the incident. In October 2001, Yates was sentenced to 10 months in prison after admitting handling the stolen machine and demanding ransom for its return, although he maintained that he was acting as an intermediary for a third party.[42] Yates was released from prison after serving three months.

In October 2008, the Spanish daily newspaper El País reported that 28 Enigma machines had been discovered by chance in an attic of the Army headquarters in Madrid during inventory taking. These 4-rotor commercial machines had helped Franco's Nationalists win the Spanish Civil War because, although the British code breaker Alfred Dilwyn Knox broke the code generated by Franco's Enigma machines in 1937, this was not disclosed to the Republicans and they could not break the code. The Nationalist government continued to use Enigma machines into the 1950s, eventually having a total of 50. Some of the 28 machines are now on display in Spanish military museums.[43]

Derivatives

The Enigma was influential in the field of cipher machine design, and a number of other rotor machines are derived from it. The British Typex was originally derived from the Enigma patents; Typex even includes features from the patent descriptions that were omitted from the actual Enigma machine. Owing to the need for secrecy about its cipher systems, no royalties were paid for the use of the patents by the British government. The Typex implementation of the Enigma transform is not the same as the transform found in almost all of the German or other Axis implementations of the machine.

A Japanese Enigma clone was codenamed GREEN by American cryptographers. Little used, it contained four rotors mounted vertically. In the U.S., cryptologist William Friedman designed the M-325, a machine similar to Enigma in logical operation, although not in construction.

A unique rotor machine was constructed in 2002 by Netherlands-based Tatjana van Vark. This unusual device was inspired by Enigma but makes use of 40-point rotors, allowing letters, numbers and some punctuation to be used; each rotor contains 509 parts.[44]

Machines like the SIGABA, NEMA, Typex and so forth, are deliberately not considered to be Enigma derivatives as their internal ciphering functions are not mathematically identical to the Enigma transform.

Several software implementations of Enigma machines do exist, but not all are state machine compliant with the Enigma family. The most commonly used software derivative (that is not compliant with any hardware implementation of the Enigma) is at Enigma.co.de. Many Java applet Enigmas only accept single letter entry, making use difficult even if the applet is Enigma state machine compliant. Technically Enigma@home is the largest scale deployment of a software Enigma, but the decoding software does not implement encipherment making it a derivative (as all original machines could cipher and decipher).

On the other hand, there is a very user-friendly 3-rotor simulator here: http://w1tp.com/enigma/enigma_w.zip where users can select rotors, use the plugboard as well as defining new settings to the rotors and reflectors. The output is in separate windows which can be independently made "invisible" to hide decryption. A 32-bit version of this simulator can be found here : http://membres.lycos.fr/pc1/enigma

A more complex version is here: http://w1tp.com/enigma/EnigmaSim.zip which includes an "autotyping" function which takes plaintext from a clipboard and converts it to cyphertext (or vice-versa) at one of four speeds. The "very fast" option runs through 26 characters in less than one second.

There currently are no known open source projects to implement the Enigma in logic gates using either RTL or VHDL logic gate markup languages.


Fiction

The play Breaking the Code, dramatised by Hugh Whitemore, is about the life and death of Alan Turing, who was the central force in continuing to break the Enigma in Britain during World War II. Turing was played by Derek Jacobi, who also played Turing in a 1996 television adaptation of the play. Although it is a drama and thus takes artistic license, it is nonetheless a fundamentally accurate account.

Robert Harris's 1995 novel Enigma is set against the backdrop of World War II Bletchley Park and cryptologists working to read Naval Enigma in Hut 8. The book, with substantial changes in plot, was made into the 2001 film Enigma, directed by Michael Apted and starring Kate Winslet and Dougray Scott. The film has been criticized for many historical inaccuracies, including neglect of the role of Poland's Biuro Szyfrów in breaking the Enigma cipher and showing the British how to do it. The film—like the book—makes a Pole the villain, who seeks to betray the secret of Enigma decryption.[45]

An earlier Polish film dealing with Polish aspects of the subject was the 1979 Sekret Enigmy, whose title translates as The Enigma Secret.[46]

Wolfgang Petersen's 1981 film Das Boot includes an Enigma machine which is evidently a four-rotor Kriegsmarine variant. It appears in many scenes, which probably capture well the flavour of day-to-day Enigma use aboard a World War II U-Boat. The plot of U-571, released in 2000, revolves around an attempt to seize an Enigma machine from a German U-boat.

An Enigma machine makes a very brief appearance in the 1980s TV show Whiz Kids, episode 12.

Neal Stephenson's novel Cryptonomicon prominently features the Enigma machine and efforts by British and American cryptologists to break variants of it, and portrays the German U-boat command under Karl Dönitz using it in apparently deliberate ignorance of its having been broken.

In the comedy war film All the Queen's Men, released in 2001 and starring Matt LeBlanc alongside Eddie Izzard, four World War II Allied soldiers are parachuted into Germany, where, dressed as women, they attempt to steal an Enigma machine. They eventually learn that the Allies already had the machine and that the mission was a ruse intended to mislead the Germans into thinking that Enigma was a closed book to the Allies.

EnigmaWarsaw is an outdoor city game in Warsaw organised by StayPoland travel agency. This treasure hunt game is devised to help the players imagine pre-war Warsaw. EnigmaWarsaw is named to commemorate the pioneering work of Polish cryptographers Marian Rejewski, Jerzy Różycki, and Henryk Zygalski at decrypting the Enigma machine cipher.

To Say Nothing of the Dog is a science fiction novel about time traveling historians in which the importance of the Allies obtaining the German Enigma machine is heavily stressed.

In the TV show Sanctuary, the deciphering of the Enigma cipher is credited to Nikola Tesla during the episode "Into the Black", released on June 20, 2011.

In Ian Fleming's From Russia with Love, released in 1957, the fictitious Spektor code machine, based on the real-life Enigma cipher machine, is used as a plot piece. This device would supposedly intercept Russian coded traffic and decipher it, allowing MI6's cryptanalysts to access decoded information.

Notes

  1. ^ Singh, Simon (1999). The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography. London: Fourth Estate. p. 127. ISBN 1-85702-879-1. 
  2. ^ Lord, Bob (1998–2010). "1937 Enigma Manual by: Jasper Rosal - English Translation". http://www.ilord.com/enigma-manual1937-english.html. Retrieved 31 May 2011 
  3. ^ http://www.codesandciphers.org.uk/virtualbp/poles/poles.htm
  4. ^ Peter, Laurence (20 July 2009). "How Poles cracked Nazi Enigma secret". BBC News. http://news.bbc.co.uk/2/hi/europe/8158782.stm. 
  5. ^ Gordon Welchman, who became head of Hut 6 at Bletchley Park, has written: "Hut 6 Ultra would never have gotten off the ground if we had not learned from the Poles, in the nick of time, the details both of the German military version of the commercial Enigma machine, and of the operating procedures that were in use." Gordon Welchman, The Hut Six Story, 1982, p. 289.
  6. ^ Much of the German cipher traffic was encrypted on the Enigma machine, hence the term "Ultra" has often been used almost synonymously with "Enigma decrypts". However, Ultra also encompassed decrypts of the German Lorenz SZ 40 and 42 machines that were used by the German High Command, and decrypts of Hagelin ciphers and of other Italian ciphers and codes, as well as of Japanese ciphers and codes such as Purple and JN-25.
  7. ^ Kahn (1991).
  8. ^ a b Miller, A. Ray (2001). The Cryptographic Mathematics of Enigma. National Security Agency. http://www.nsa.gov/about/_files/cryptologic_heritage/publications/wwii/engima_cryptographic_mathematics.pdf 
  9. ^ Bletchley Park veteran and historian F.H. Hinsley is often cited as an authority for the two-year estimate, yet his assessment in Codebreakers is much less definitive: "Would the Soviets meanwhile have defeated Germany, or Germany the Soviets, or would there have been stalemate on the eastern fronts? What would have been decided about the atom bomb? Not even counter-factual historians can answer such questions. They are questions which do not arise, because the war went as it did. But those historians who are concerned only with the war as it was must ask why it went as it did. And they need venture only a reasonable distance beyond the facts to recognise the extent to which the explanation lies in the influence of Ultra." F.H. Hinsley, "Introduction: The Influence of Ultra in the Second World War," Codebreakers: The Inside Story of Bletchley Park, edited by F.H. Hinsley and Alan Stripp, Oxford University Press, 1993, pp. 12–13.
  10. ^ http://www.history.co.uk/explore-history/ww2/code-breaking.html
  11. ^ Kahn (1991), Hinsley and Stripp (1993).
  12. ^ a b c Rijmenants, Dirk; Technical details of the Enigma machine Cipher Machines & Cryptology
  13. ^ a b c David Hamer, "Enigma: Actions Involved in the 'Double-Stepping' of the Middle Rotor", Cryptologia, 21(1), January 1997, pp. 47–50, Online version (zipped PDF)
  14. ^ Sale, Tony. "Technical specifications of the Enigma rotors". Technical Specification of the Enigma. http://www.codesandciphers.org.uk/enigma/rotorspec.htm. Retrieved 2009-11-15. 
  15. ^ http://www.cryptomuseum.com/crypto/enigma/lf/index.htm
  16. ^ Philip Marks, "Umkehrwalze D: Enigma's Rewirable Reflector — Part I", Cryptologia 25(2), April 2001, pp. 101–141
  17. ^ Reuvers, Paul (2008). "Enigma accessories". http://www.jproc.ca/crypto/enigma_acc.html. Retrieved 22 July 2010 
  18. ^ Rejewski 1980
  19. ^ Friedman, W.F. (1922). The index of coincidence and its applications in cryptology. Department of Ciphers. Publ 22. Geneva, Illinois, USA: Riverbank Laboratories. OCLC 55786052. 
  20. ^ Rijmenants, Dirk; Enigma message procedures Cipher Machines & Cryptology
  21. ^ Rijmenants, Dirk; Kurzsignalen on German U-boats Cipher Machines & Cryptology
  22. ^ "The translated 1940 Enigma General Procedure". codesandciphers.org.uk. http://www.codesandciphers.org.uk/documents/egenproc/eniggnix.htm. Retrieved 2006-10-16. 
  23. ^ "The translated 1940 Enigma Officer and Staff Procedure". codesandciphers.org.uk. http://www.codesandciphers.org.uk/documents/officer/officerx.htm. Retrieved 2006-10-16. 
  24. ^ "image of Enigma Type B". http://www.armyradio.com/publish/Articles/The_Enigma_Code_Breach/Pictures/enigma_type_b.jpg. 
  25. ^ Kahn, 1991, pp. 39–41, 299
  26. ^ Ulbricht, 2005, p.4
  27. ^ a b Stripp, 1993
  28. ^ Kahn, 1991, pp. 40, 299
  29. ^ Bauer, 2000, p. 108
  30. ^ Hinsley and Stripp, 1993, plate 3
  31. ^ Kahn, 1991, pp. 41, 299
  32. ^ a b c d Deavours and Kruh, 1985, p. 97
  33. ^ Michael Smith Station X, four books (macmillan) 1998, Paperback 2000, ISBN 0-7522-7148-2, Page 73
  34. ^ Kahn, 1991, p. 43
  35. ^ Kahn (1991, p. 43) says August 1934. Kruh and Deavours (2002, p. 15) say October 2004.
  36. ^ a b Deavours and Kruh, 1985, p. 98
  37. ^ Kozaczuk, 1984, p. 28.
  38. ^ Smith 2006, p. 23
  39. ^ a b Bauer, 2000, p. 112
  40. ^ Hamer, David; Enigma machines - known locations*
  41. ^ Hamer, David; Selling prices of Enigma and NEMA - all prices converted to US$
  42. ^ "Man jailed over Enigma machine". BBC News. 19 October 2001. http://news.bbc.co.uk/1/hi/uk/1609168.stm. Retrieved 2 May 2010. 
  43. ^ Graham Keeley. Nazi Enigma machines helped General Franco in Spanish Civil War The Times 24 October 2008. p 47
  44. ^ van Vark, Tatjana The coding machine
  45. ^ Laurence Peter, How Poles cracked Nazi Enigma secret, BBC News, 20 July 2009
  46. ^ Sekret Enigmy (Film 1979) Internet Movie Database

References

  • Bauer, F. L. (2000). Decrypted Secrets (Springer, 2nd edition). ISBN 3-540-66871-3
  • Hamer, David H.; Sullivan, Geoff; Weierud, Frode (July 1998). "Enigma Variations: an Extended Family of Machines", Cryptologia, 22(3). Online version (zipped PDF).
  • Stripp, Alan. "The Enigma Machine: Its Mechanism and Use" in Hinsley, F. H.; and Stripp, Alan (editors), Codebreakers: The Inside Story of Bletchley Park (1993), pp. 83–88.
  • Kahn, David (1991). Seizing the Enigma: The Race to Break the German U-Boats Codes, 1939-1943 ISBN 0-395-42739-8.
  • Kozaczuk, Władysław, Enigma: How the German Machine Cipher Was Broken, and How It Was Read by the Allies in World War Two, edited and translated by Christopher Kasparek, Frederick, MD, University Publications of America, 1984, ISBN 0-89093-547-5.
  • Kozaczuk, Władysław. The origins of the Enigma/ULTRA
  • Kruh, Louis; Deavours, Cipher (2002). "The Commercial Enigma: Beginnings of Machine Cryptography", Cryptologia, 26(1), pp. 1–16. Online version (PDF)
  • Marks, Philip; Weierud, Frode (January 2000). "Recovering the Wiring of Enigma's Umkehrwalze A", Cryptologia 24(1), pp55–66.
  • Rejewski, Marian (1980). "An Application of the Theory of Permutations in Breaking the Enigma Cipher". Applicationes mathematicae 16 (4). ISSN 1730-6280. http://cryptocellar.org/ 
  • Smith, Michael (1998). Station X (Macmillan) ISBN 0-7522-7148-2
  • Smith, Michael (2006). "How it began: Bletchley Park Goes to War". In Copeland, B Jack. Colossus: The Secrets of Bletchley Park's Codebreaking Computers. Oxford: Oxford University Press. ISBN 978-0-19-284055-4 
  • Ulbricht, Heinz. Die Chiffriermaschine Enigma — Trügerische Sicherheit: Ein Beitrag zur Geschichte der Nachrichtendienste, PhD Thesis, 2005. Online version.(German)

Further reading

  • Richard J. Aldrich, GCHQ: The Uncensored Story of Britain's Most Secret Intelligence Agency, HarperCollins, July 2010.
  • Calvocoressi, Peter. Top Secret Ultra. Baldwin, new edn 2001. 978-0-947712-36-5
  • Cave Brown, Anthony. Bodyguard of Lies, 1975. A journalist's sensationalist best-seller that purported to give a history of Enigma decryption and its effect on the outcome of World War II. Worse than worthless on the seminal Polish work that made "Ultra" possible. See Richard Woytak, prefatory note (pp. 75–76) to Marian Rejewski, "Remarks on Appendix 1 to British Intelligence in the Second World War by F.H. Hinsley", Cryptologia, vol. 6, no. 1 (January 1982), pp. 76–83.
  • Garliński, Józef Intercept, Dent, 1979. A superficial, sometimes misleading account of Enigma decryption before and during World War II, of equally slight value as to both the Polish and British phases. See Richard Woytak and Christopher Kasparek, "The Top Secret of World War II", The Polish Review, vol. XXVIII, no. 2, 1983, pp. 98–103 (specifically, about Garliński, pp. 101–3).
  • Herivel, John. Herivelismus and the German military Enigma. Baldwin, 2008. 978-0-947712-46-4
  • Keen, John. Harold 'Doc' Keen and the Bletchley Park Bombe. Baldwin, 2003. 978-0-947712-42-6
  • Large, Christine. Hijacking Enigma, 2003, ISBN 0-470-86347-1.
  • Marks, Philip. "Umkehrwalze D: Enigma's Rewirable Reflector—Part I", Cryptologia 25(2), April 2001, pp. 101–141.
  • Marks, Philip. "Umkehrwalze D: Enigma's Rewirable Reflector—Part II", Cryptologia 25(3), July 2001, pp. 177–212.
  • Marks, Philip. "Umkehrwalze D: Enigma's Rewirable Reflector—Part III", Cryptologia 25(4), October 2001, pp. 296–310.
  • Perera, Tom. The Story of the ENIGMA: History, Technology and Deciphering, 2nd Edition, CD-ROM, 2004, Artifax Books, ISBN 1-890024-06-6 sample pages
  • Rejewski, Marian. "How Polish Mathematicians Deciphered the Enigma", Annals of the History of Computing 3, 1981. This article is regarded by Andrew Hodges, Alan Turing's biographer, as "the definitive account" (see Hodges' Alan Turing: The Enigma, Walker and Company, 2000 paperback edition, p. 548, footnote 4.5).
  • Quirantes, Arturo. "Model Z: A Numbers-Only Enigma Version", Cryptologia 28(2), April 2004.
  • Sebag-Montefiore, Hugh. Enigma: the battle for the code. Cassell Military Paperbacks, London, 2004. 978-1-407-22129-8
  • Ulbricht, Heinz. Enigma Uhr, Cryptologia, 23(3), April 1999, pp. 194–205.
  • Welchman, Gordon. The Hut Six Story: breaking the Enigma codes. Baldwin, new edition, 1997. 978-0-947712-34-1
  • Winterbotham, F.W, The Ultra Secret, Harper and Row, New York, 1974; Spanish edition Ultrasecreto, Ediciones Grijalbo, Madrid, 1975

External links


 
Cipher machines
Rotor machines:
Mechanical:
Teleprinter:
Secure voice:
Miscellaneous: